Enumerations of Permutations Simultaneously Avoiding a Vincular and a Covincular Pattern of Length 3
Journal of Integer Sequences, Volume 20 (2017), Article 17.7.6
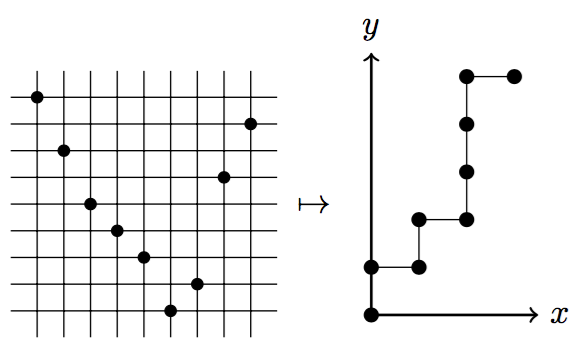A pattern is said to be covincular if its inverse is vincular. In this paper we
count the number of permutations simultaneously avoiding a vincular and a
covincular pattern, both of length 3. We see familiar sequences, such as the
Catalan and Motzkin numbers, but also some previously unknown sequences which
have close links to other combinatorial objects such as ascent sequences,
lattice paths and integer partitions. Where possible we include a generating
function for the enumeration. We also give an alternative proof of the classic
result that permutations avoiding 123 are counted by the Catalan numbers.