-
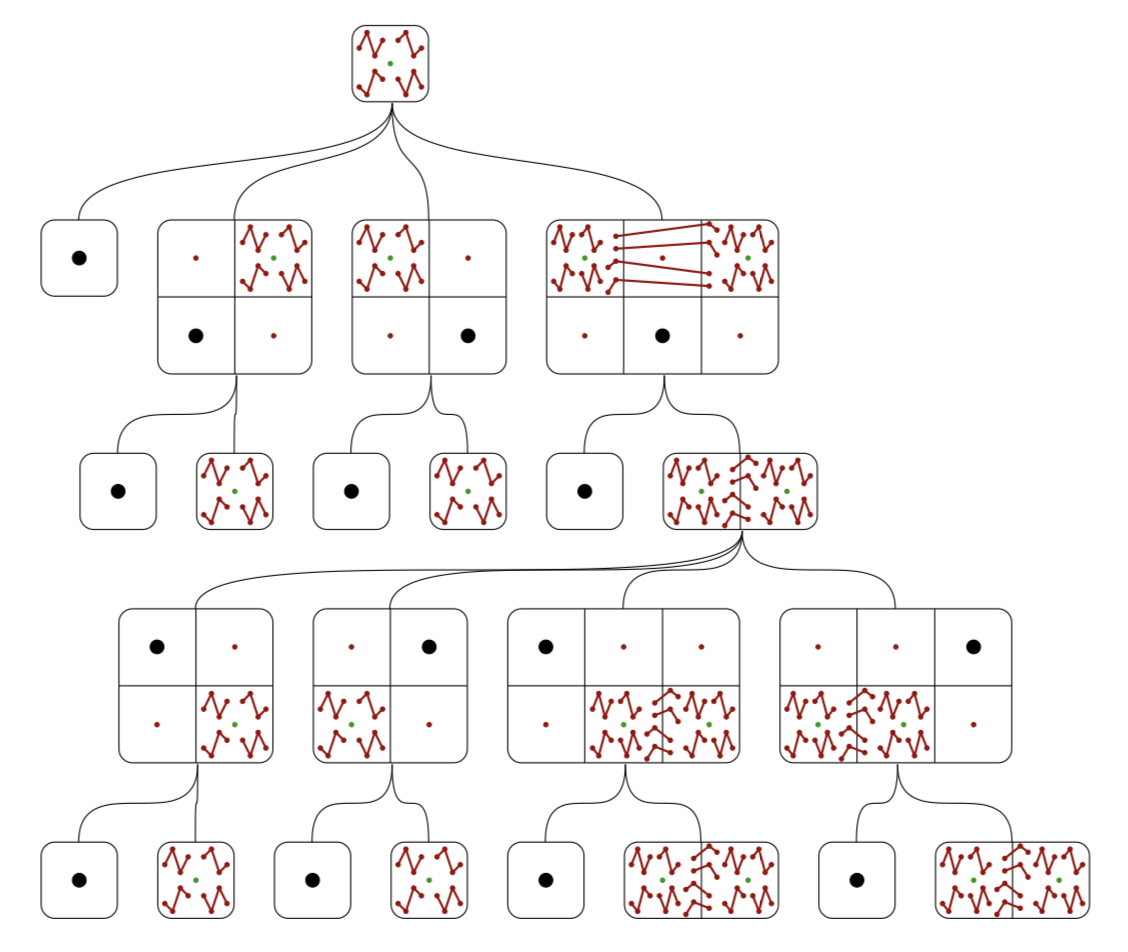 A combinatorial class is often studied by finding a combinatorial specification
for it, which is a description of the class in terms of simpler classes, and
perhaps recursions to smaller instances of the original class.
This project aims to automate the discovery of combinatorial specifications
of combinatorial classes. This is achieved by first generating a universe of
interconnected combinatorial classes and then searching for a specification
inside this universe. The main application has been in the area of permutation
patterns, but other domains such as, set partitions, strings, polyominoes and
lattice paths have been considered.
A combinatorial class is often studied by finding a combinatorial specification
for it, which is a description of the class in terms of simpler classes, and
perhaps recursions to smaller instances of the original class.
This project aims to automate the discovery of combinatorial specifications
of combinatorial classes. This is achieved by first generating a universe of
interconnected combinatorial classes and then searching for a specification
inside this universe. The main application has been in the area of permutation
patterns, but other domains such as, set partitions, strings, polyominoes and
lattice paths have been considered.
-
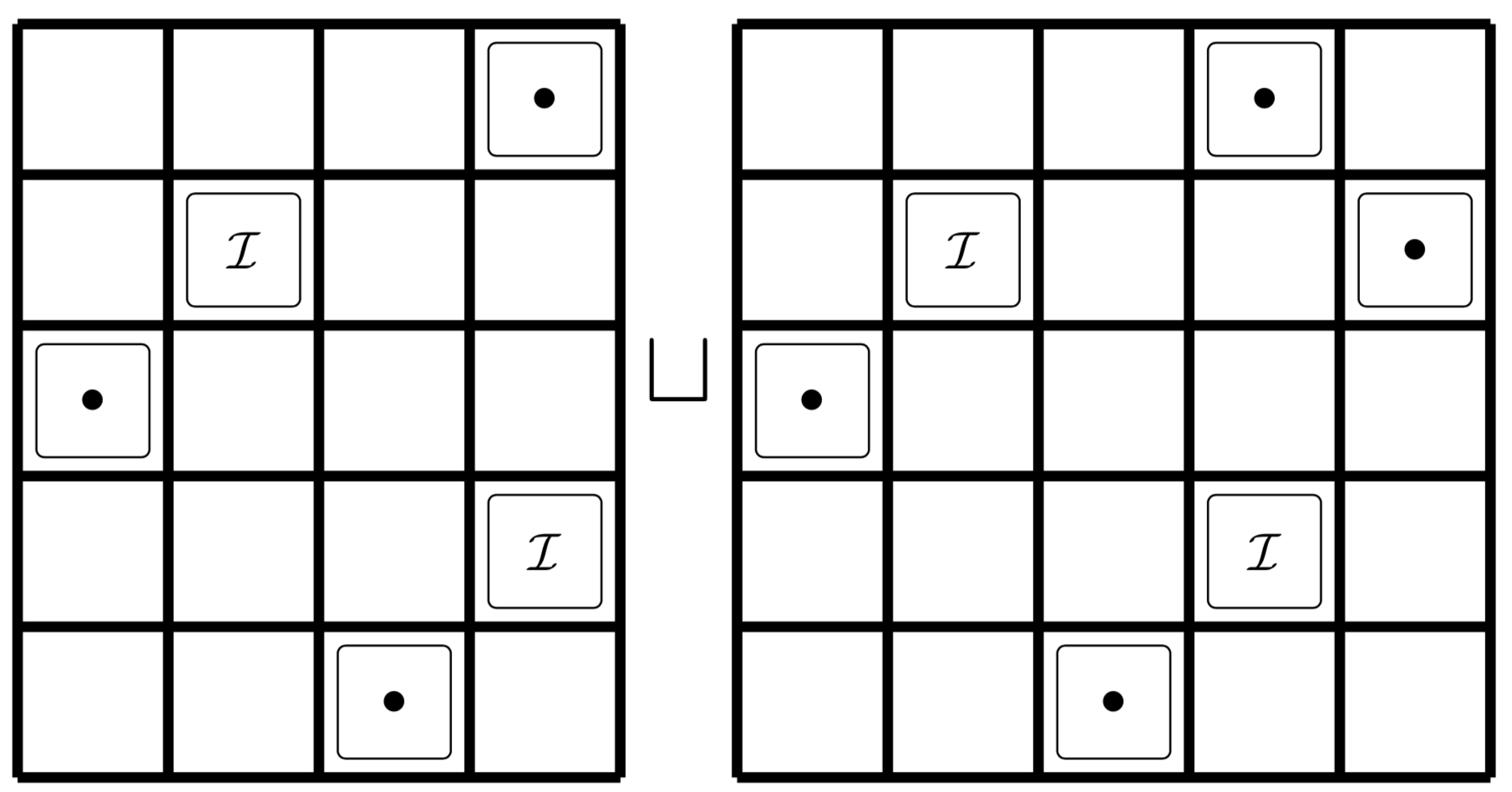 This project started with an IRF grant in 2014 and the hiring of
Christian as a PhD student.
The idea is to guess an exact cover a combinatorial class. Currently we have
a program that does this in the case of a permutation class.
This project started with an IRF grant in 2014 and the hiring of
Christian as a PhD student.
The idea is to guess an exact cover a combinatorial class. Currently we have
a program that does this in the case of a permutation class.
-
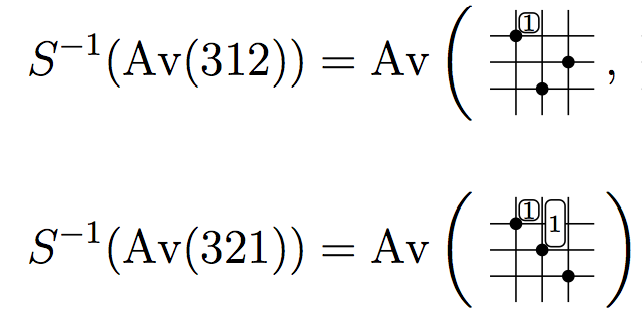 We introduce an algorithm to determine when a sorting operation, such as
stack-sort or bubble-sort, outputs a given pattern. The algorithm provides a
new proof of the description of West-2-stack-sortable permutations, that is
permutations that are completely sorted when passed twice through a stack, in
terms of patterns. We also solve the long-standing problem of describing
West-3-stack-sortable permutations. This requires a new type of generalized
permutation pattern we call a decorated pattern.
We introduce an algorithm to determine when a sorting operation, such as
stack-sort or bubble-sort, outputs a given pattern. The algorithm provides a
new proof of the description of West-2-stack-sortable permutations, that is
permutations that are completely sorted when passed twice through a stack, in
terms of patterns. We also solve the long-standing problem of describing
West-3-stack-sortable permutations. This requires a new type of generalized
permutation pattern we call a decorated pattern.
-
 We study algorithms that given a finite set of permutations conjecture (1) a
basis of (mesh) patterns describing the set; (2) a structural description of
the set, that can then be translated into a generating function enumerating the
set.
We study algorithms that given a finite set of permutations conjecture (1) a
basis of (mesh) patterns describing the set; (2) a structural description of
the set, that can then be translated into a generating function enumerating the
set.
-
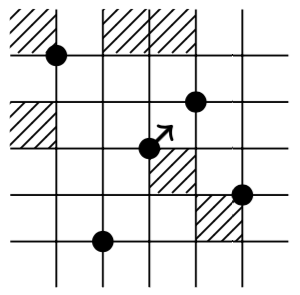 Two patterns are coincident if they are avoided by the same permutations. They
are Wilf-equivalent if the are avoided by the same number of permutations. We
study general rules which can tell us when patterns (or sets of patterns) are
coincident or Wilf-equivalent.
Two patterns are coincident if they are avoided by the same permutations. They
are Wilf-equivalent if the are avoided by the same number of permutations. We
study general rules which can tell us when patterns (or sets of patterns) are
coincident or Wilf-equivalent.
-
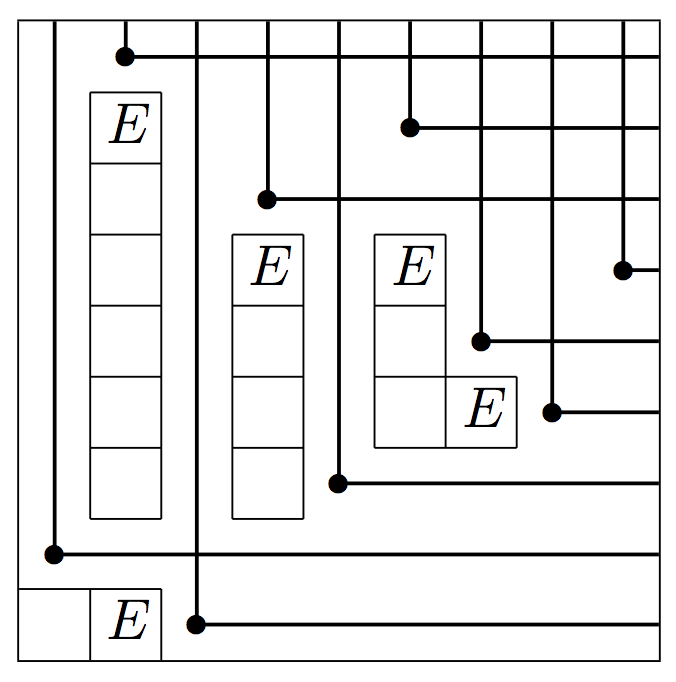 Description.
Description.
 A combinatorial class is often studied by finding a combinatorial specification
for it, which is a description of the class in terms of simpler classes, and
perhaps recursions to smaller instances of the original class.
This project aims to automate the discovery of combinatorial specifications
of combinatorial classes. This is achieved by first generating a universe of
interconnected combinatorial classes and then searching for a specification
inside this universe. The main application has been in the area of permutation
patterns, but other domains such as, set partitions, strings, polyominoes and
lattice paths have been considered.
A combinatorial class is often studied by finding a combinatorial specification
for it, which is a description of the class in terms of simpler classes, and
perhaps recursions to smaller instances of the original class.
This project aims to automate the discovery of combinatorial specifications
of combinatorial classes. This is achieved by first generating a universe of
interconnected combinatorial classes and then searching for a specification
inside this universe. The main application has been in the area of permutation
patterns, but other domains such as, set partitions, strings, polyominoes and
lattice paths have been considered. This project started with an IRF grant in 2014 and the hiring of
Christian as a PhD student.
The idea is to guess an exact cover a combinatorial class. Currently we have
a program that does this in the case of a permutation class.
This project started with an IRF grant in 2014 and the hiring of
Christian as a PhD student.
The idea is to guess an exact cover a combinatorial class. Currently we have
a program that does this in the case of a permutation class.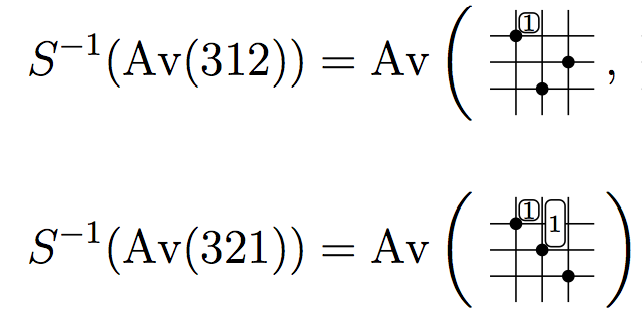 We introduce an algorithm to determine when a sorting operation, such as
stack-sort or bubble-sort, outputs a given pattern. The algorithm provides a
new proof of the description of West-2-stack-sortable permutations, that is
permutations that are completely sorted when passed twice through a stack, in
terms of patterns. We also solve the long-standing problem of describing
West-3-stack-sortable permutations. This requires a new type of generalized
permutation pattern we call a decorated pattern.
We introduce an algorithm to determine when a sorting operation, such as
stack-sort or bubble-sort, outputs a given pattern. The algorithm provides a
new proof of the description of West-2-stack-sortable permutations, that is
permutations that are completely sorted when passed twice through a stack, in
terms of patterns. We also solve the long-standing problem of describing
West-3-stack-sortable permutations. This requires a new type of generalized
permutation pattern we call a decorated pattern. We study algorithms that given a finite set of permutations conjecture (1) a
basis of (mesh) patterns describing the set; (2) a structural description of
the set, that can then be translated into a generating function enumerating the
set.
We study algorithms that given a finite set of permutations conjecture (1) a
basis of (mesh) patterns describing the set; (2) a structural description of
the set, that can then be translated into a generating function enumerating the
set. Two patterns are coincident if they are avoided by the same permutations. They
are Wilf-equivalent if the are avoided by the same number of permutations. We
study general rules which can tell us when patterns (or sets of patterns) are
coincident or Wilf-equivalent.
Two patterns are coincident if they are avoided by the same permutations. They
are Wilf-equivalent if the are avoided by the same number of permutations. We
study general rules which can tell us when patterns (or sets of patterns) are
coincident or Wilf-equivalent. Description.
Description.