Papers

• Turning cycle restrictions into mesh patterns via Foata's fundamental transformation

  Submitted

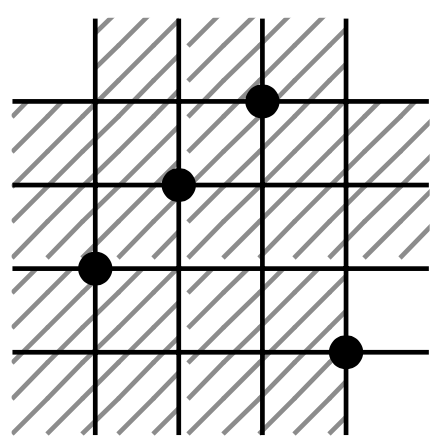  An adjacent q-cycle is a natural generalization of an adjacent transposition. We show that the number of adjacent q-cycles in a permutation maps to the sum of occurrences of two mesh patterns under Foata’s fundamental transformation. As a corollary we resolve Conjecture 3.14 in the paper ‘‘From Hertzprung’s problem to pattern-rewriting systems’’ by the first author. This work was started at Schloss Dagstuhl (Leibniz-Zentrum fur Informatik), seminar 23121, and we thank the institute and the organizers for giving us the opportunity to participate.

• Pattern avoiding Motzkin paths are almost rational

  Submitted

  Using a recursive approach, we show that the generating function for sets of Motzkin paths avoiding a single (not necessarily consecutive) pattern is rational over x and the Catalan generating function C(x). Moreover, an algorithm is provided for finding the generating function, also in the more general case of an arbitrary set of patterns. In addition, such an algorithm allows us to find a combinatorial specification for pattern avoiding Motzkin paths, which can be used not only for enumeration, but also for exhaustive and random generation.

• Automated Enumeration of Combinatorial Classes with Proof-Number Search

  Submitted 2019

  Enumerative combinatorics has traditionally been the domain of work for human mathematicians and has been applied, for instance with the probabilistic method, in computer science. One of the main problems in enumerative combinatorics is the counting of combinatorial classes, and in recent years, efforts have been made to write algorithms to solve such problems. We show that these automated methods may benefit from the application of already mature AI algorithms, such as Proof-Number Search.

• Enumeration of Permutation Classes and Weighted Labelled Independent Sets

  Discrete Mathematics & Theoretical Computer Science, vol. 22 no. 2, Permutation Patterns 2019.

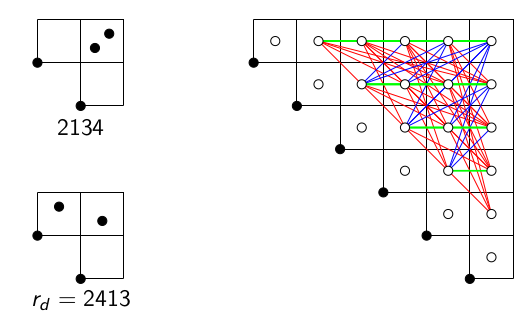  In this paper, we study the staircase encoding of permutations, which maps a permutation to a staircase grid with cells filled with permutations. We consider many cases, where restricted to a permutation class, the staircase encoding becomes a bijection to its image. We describe the image of those restrictions using independent sets of graphs weighted with permutations. We derive the generating function for the independent sets and then for their weighted counterparts. The bijections we establish provide the enumeration of permutation classes. We use our results to uncover some unbalanced Wilf-equivalences of permutation classes and outline how to do random sampling in the permutation classes. In particular, we cover the classes Av(2314,3124) , Av(2413,3142), Av(2413,3124), Av(2413,2134) and Av(2314,2143), as well as many subclasses.

• Algorithmic coincidence classification of mesh patterns

  Submitted

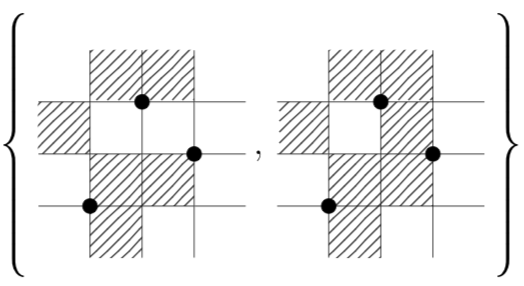  We introduce the concept of a force on a permutation pattern and use it to strengthen previous results on coincidence classification of mesh patterns. By creating an algorithm that recursively applies our results we are able to automatically coincidence classify mesh patterns of length less than 3.

• Combinatorial Exploration: An Algorithmic Framework for Enumeration

  Submitted

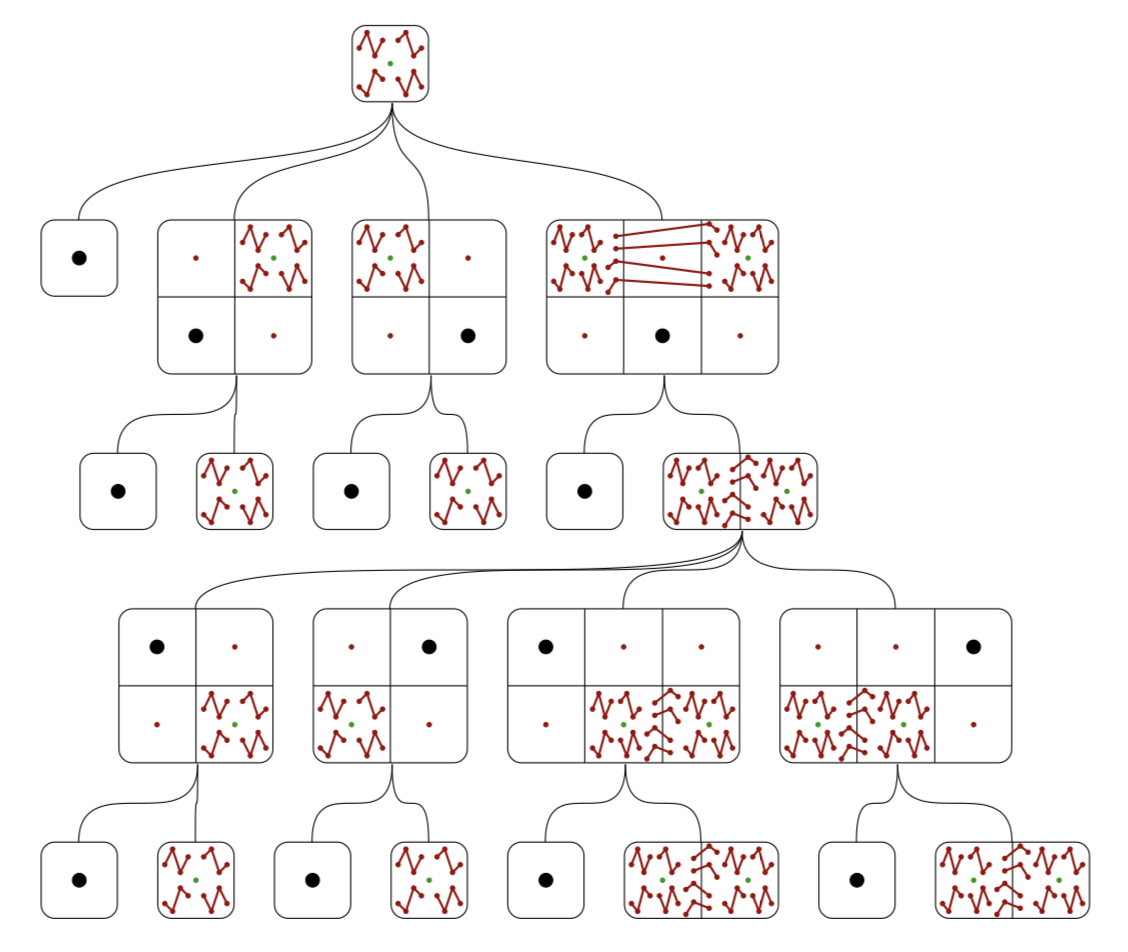  A combinatorial class is often studied by finding a combinatorial specification for it, which is a description of the class in terms of simpler classes, and perhaps recursions to smaller instances of the original class. In this paper we describe how to automate the discovery of combinatorial specifications of combinatorial classes. This is achieved by first generating a universe of interconnected combinatorial classes and then searching for a specification inside this universe. The main application is in the area of permutation patterns, but other domains such as, set partitions, strings, polyominoes and lattice paths are discussed considered.

• The poset of mesh patterns

  Discrete Mathematics, Volume 343, Issue 6, June 2020

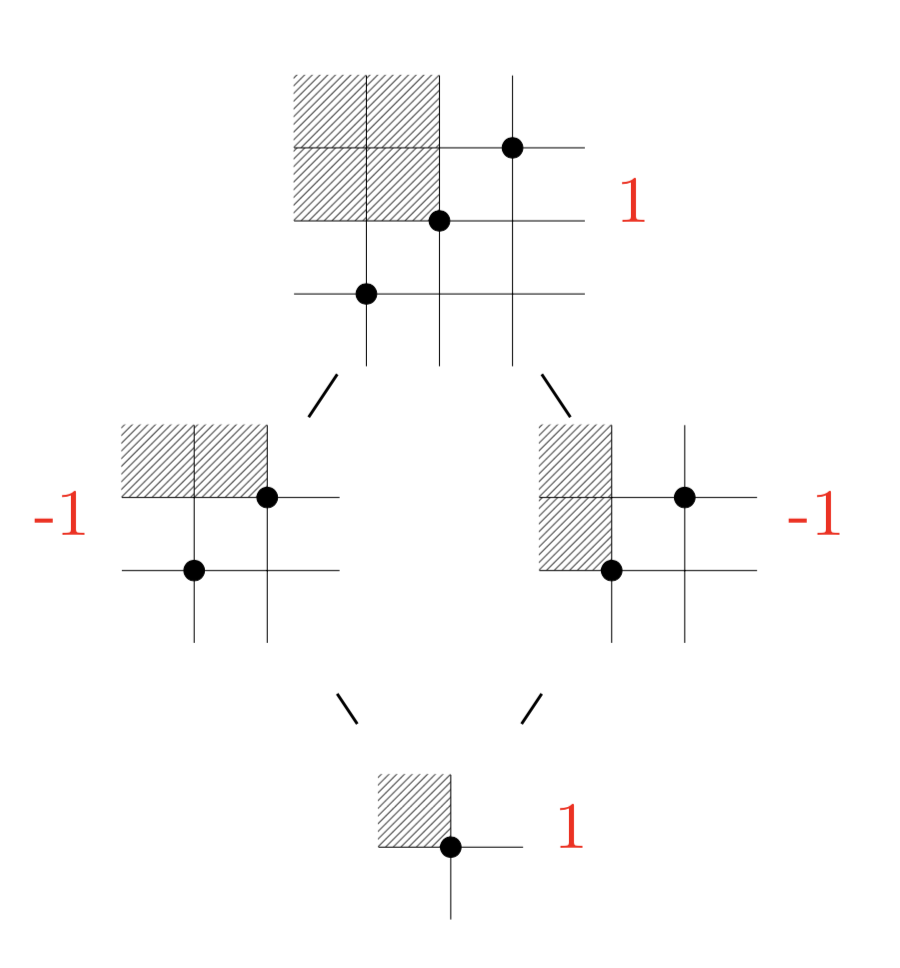  We introduce the poset of mesh patterns, which generalises the permutation pattern poset. We fully classify the mesh patterns for which the interval [1,m] is non-pure, where 1 is the unshaded singleton mesh pattern. We present some results on the Möbius function of the poset, and show that its value on [1,m] is almost always zero. Finally, we introduce a class of disconnected and non-shellable intervals by generalising the direct product operation from permutations to mesh patterns.

• Collatz meets Fibonacci

  The MAA Mathematics Magazine, Volume 95, 2022 - Issue 2, p. 130-136

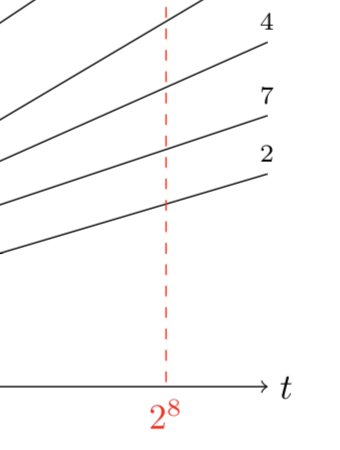  The Collatz map is defined for a positive even integer as half that integer, and for a positive odd integer as that integer threefold, plus one. The Collatz conjecture states that when the map is iterated the number one is eventually reached. We study permutations that arise as sequences from this iteration. We show that permutations of this type of length up to 14 are enumerated by the Fibonacci numbers. Beyond that excess permutations appear. We will explain the appearance of these excess permutations and give an upper bound on the exact enumeration.

• BiSC: An algorithm for discovering generalized permutation patterns

  In preparation

  BiSC is an algorithm inspired by a question asked by Sara Billey in the talk Consequences of the Lakshmibai-Sandhya Theorem at the AWM Anniversary Conference in 2011. She asked whether one could write an algorithm for “learning marked mesh patterns”. The BiSC algorithm answers this question for mesh patterns. The name of the algorithm comes from the last name of Sara Billey, as well as the last names of Einar Steingrímsson and Anders Claesson who where also influential in the development of the algorithm.

• Pattern avoiding permutations and independent sets in graphs

  Journal of Combinatorics, Volume 4 (2020), Number 4

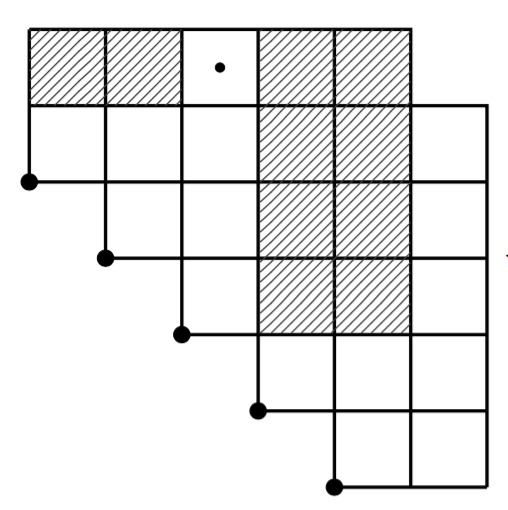  We encode certain pattern avoiding permutations as weighted independent sets in a family of graphs we call cores. For the classical case of 132-avoiding permutations we establish a bijection between the vertices of the cores and edges in a fully connected graph drawn on a convex polygon. We prove that independent sets in the core correspond to non-crossing subgraphs on the polygon, and then the well-known enumeration of these subgraphs transfers to an enumeration of 132-avoiding permutations according to left-to-right minima. We extend our results to the 123-, (1324, 2143)-, (1234, 1324, 2143)-, (1234, 1324, 1432, 3214)-avoiding permutations. We end by enumerating certain subsets of 1324-avoiding permutations that satisfy particular conditions on their left-to-right minima and right-to-left maxima.

• Occurrence graphs of patterns in permutations

  Involve, Volume 12 (2019), Number 6, 901-918

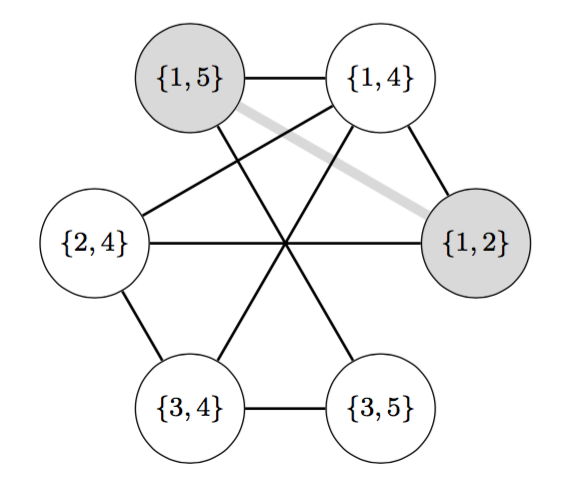  We define the occurrence graph of a pattern p in a permutation as the graph with the occurrences of p in the permutation as vertices, and edges between the vertices if the occurrences differ by exactly one element. We then study properties of these graphs. The main theorem in this paper is that every hereditary property of graphs gives rise to a permutation class.

• Automatic discovery of structural rules of permutation classes

  Mathematics of Computation, Volume 88, Number 318, July 2019, Pages 1967–1990

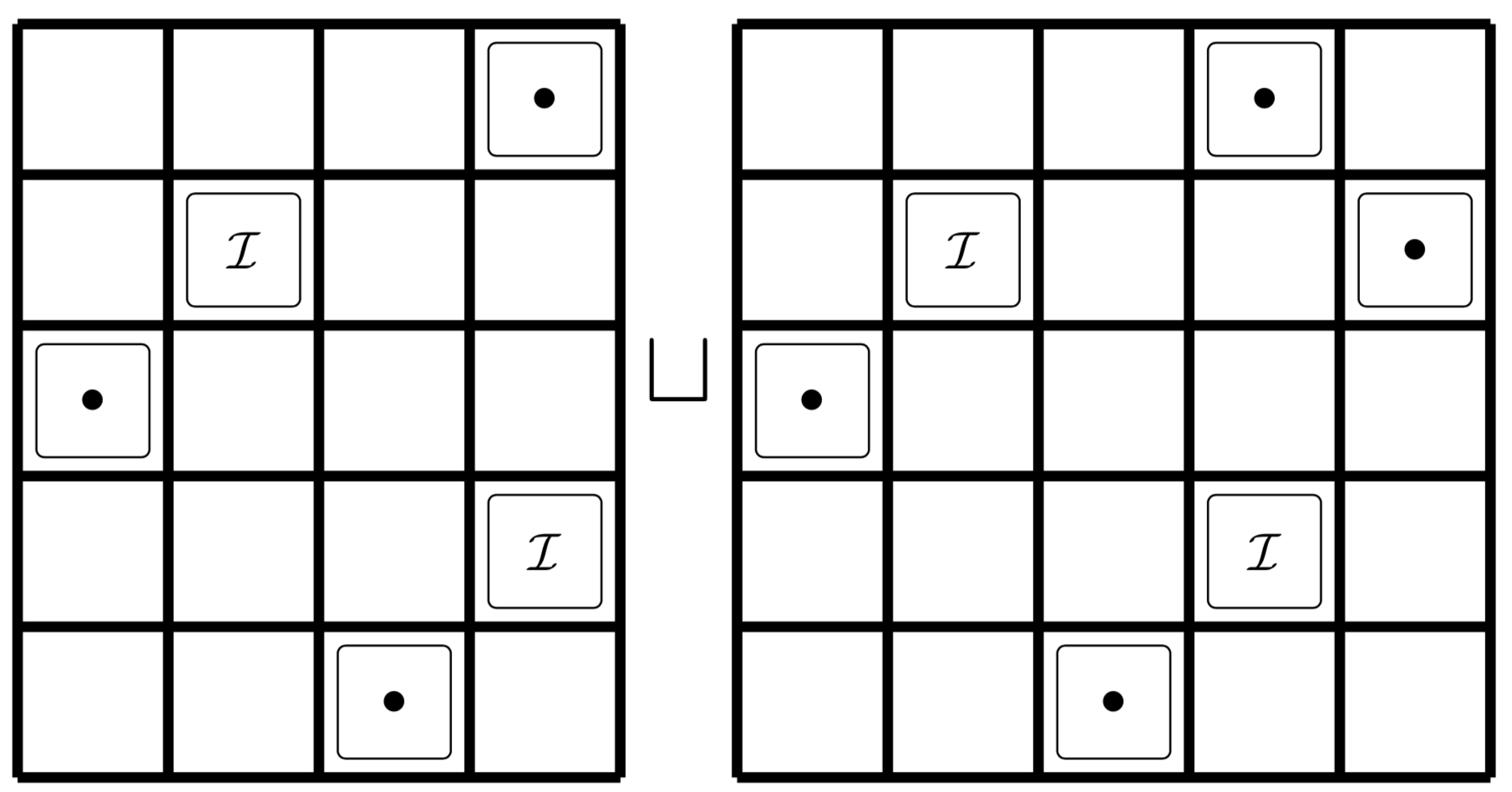  We introduce an algorithm that produces conjectures regarding the structure of permutation classes. These conjectures take the form of a disjoint cover of “rules”, each of which is similar to a generalized grid class. Such a cover is usually easily verified by a human and can often be translated directly into an enumeration. The algorithm is successful in many cases where other algorithms fail and is theoretically guaranteed to succeed on any polynomial permutation class. We apply it to every non-polynomial permutation class avoiding a set of length four patterns. The structures found by the algorithm sometimes allow one to enumerate a permutation class with respect to permutation statistics, and often yield a method for sampling uniformly at random from the class. We additionally sketch a second algorithm formalizing the human verification of the conjectured covers.

• Equivalence classes of mesh patterns with a dominating pattern

  Discrete Mathematics & Theoretical Computer Science, February 9, 2018, Vol. 19 no. 2, Permutation Patterns 2016

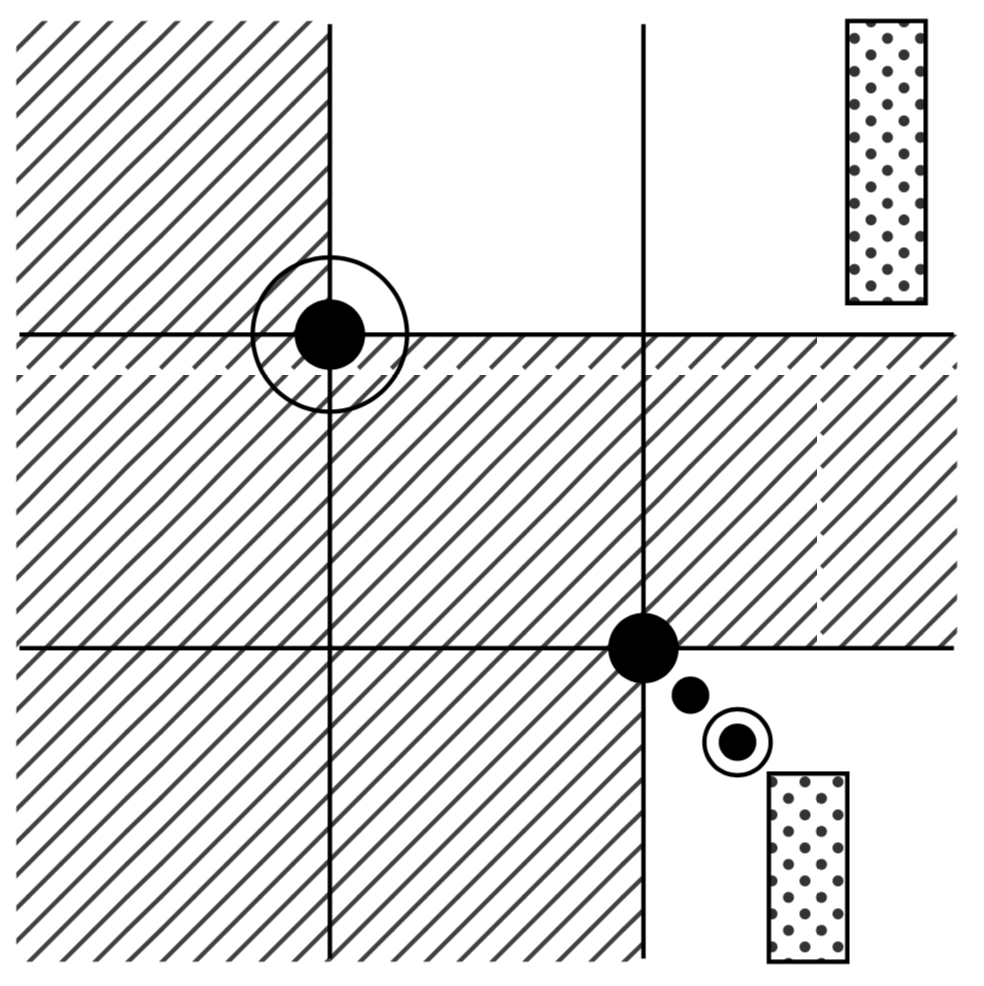  Two mesh patterns are coincident if they are avoided by the same set of permutations, and are Wilf-equivalent if they have the same number of avoiders of each length. We provide sufficient conditions for coincidence of mesh patterns, when only permutations also avoiding a longer classical pattern are considered. Using these conditions we completely classify coincidences between families containing a mesh pattern of length 2 and a classical pattern of length 3. Furthermore, we completely Wilf-classify mesh patterns of length 2 inside the class of 231-avoiding permutations.

• Enumerations of Permutations Simultaneously Avoiding a Vincular and a Covincular Pattern of Length 3

  Journal of Integer Sequences, Volume 20 (2017), Article 17.7.6

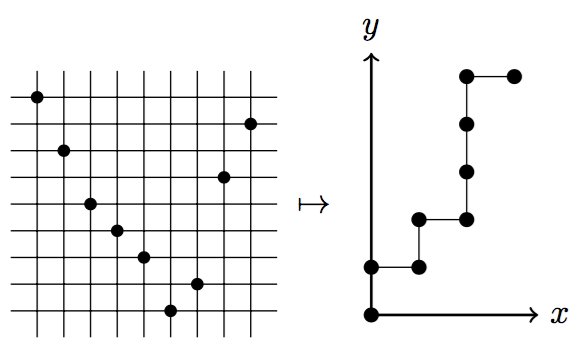  A pattern is said to be covincular if its inverse is vincular. In this paper we count the number of permutations simultaneously avoiding a vincular and a covincular pattern, both of length 3. We see familiar sequences, such as the Catalan and Motzkin numbers, but also some previously unknown sequences which have close links to other combinatorial objects such as ascent sequences, lattice paths and integer partitions. Where possible we include a generating function for the enumeration. We also give an alternative proof of the classic result that permutations avoiding 123 are counted by the Catalan numbers.

• Sorting and preimages of pattern classes

  In preparation

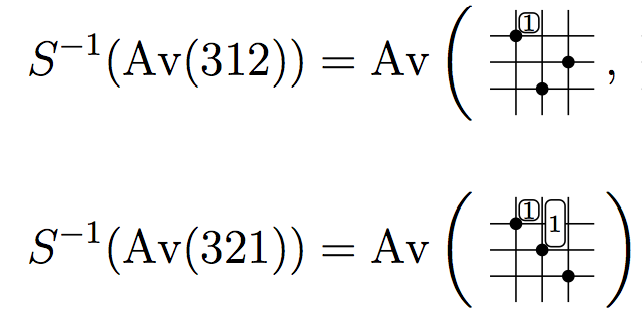  We introduce an algorithm to determine when a sorting operation, such as stack-sort or bubble-sort, outputs a given pattern. The algorithm provides a new proof of the description of West-2-stack-sortable permutations, that is permutations that are completely sorted when passed twice through a stack, in terms of patterns. We also solve the long-standing problem of describing West-3-stack-sortable permutations. This requires a new type of generalized permutation pattern we call a decorated pattern.

• Coincidence among families of mesh patterns

  The Australasian Journal of Combinatorics 2015, Volume 63 Part 1 (2015)

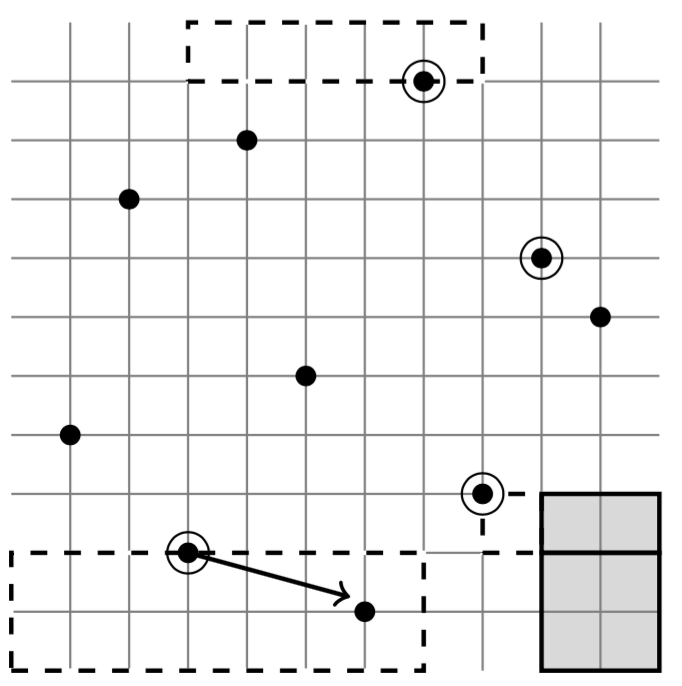  Two mesh patterns are coincident if they are avoided by the same set of permutations. In this paper, we provide necessary conditions for this coincidence, which include having the same set of enclosed diagonals. This condition is sufficient to prove coincidence of vincular patterns, although it is not enough to guarantee coincidence of bivincular patterns. In addition, we provide a generalization of the Shading Lemma (Hilmarsson et al.), a result that examined when a square could be added to the mesh of a pattern.

• Wilf-classification of mesh patterns of short length

  Electronic Journal of Combinatorics, Volume 22 (2015)

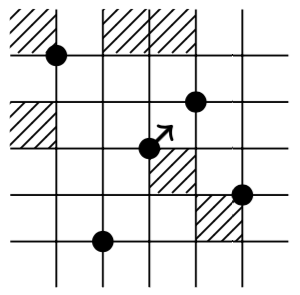  The goal of this paper is to Wilf-classify mesh patterns of length 2. To this end we prove The Shading Lemma, which gives sufficient conditions for two mesh patterns to be coincident (i.e., avoided by the same permutations) and therefore Wilf-equivalent. The lemma, along with other rules which implie Wilf-coincidence we show that there are at most 56 Wilf-classes of mesh patterns of length 2. We conjecture that the exact number is 46 and hope to revisit this area and prove this conjecture.

• Restricted non-separable planar maps and some pattern avoiding permutations

  Discrete Applied Mathematics, Volume 161, Issues 16–17, (2013), Pages 2514-2526

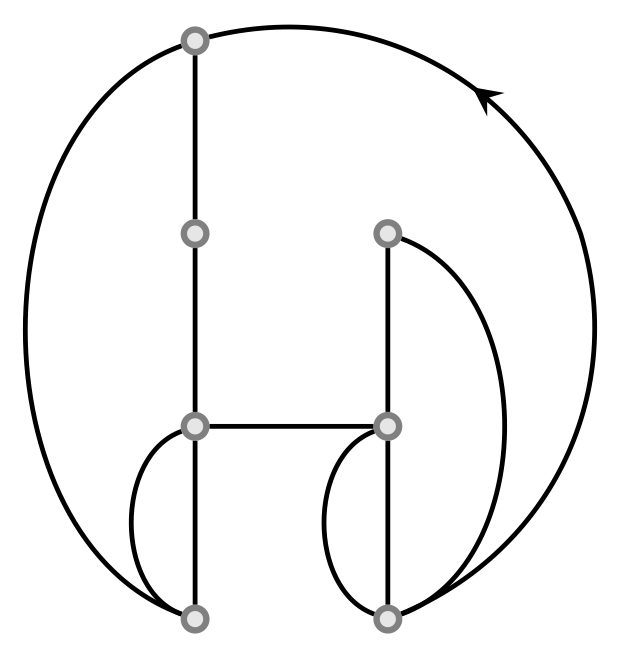  Tutte founded the theory of enumeration of planar maps in a series of papers in the 1960s. Rooted non-separable planar maps are in bijection with West-2-stack-sortable permutations, beta(1,0)-trees introduced by Cori, Jacquard and Schaeffer in 1997, as well as a family of permutations defined by the avoidance of two four letter patterns. In this paper we give upper and lower bounds on the number of multiple-edge-free rooted non-separable planar maps. We also use the bijection between rooted non-separable planar maps and a certain class of permutations, found by Claesson, Kitaev and Steingrimsson in 2009, to show that the number of 2-faces (excluding the root-face) in a map equals the number of occurrences of a certain mesh pattern in the permutations. We further show that this number is also the number of nodes in the corresponding beta(1,0)-tree that are single children with maximum label. Finally, we give asymptotics for some of our enumerative results.

• Which Schubert varieties are local complete intersections?

  Proceedings of the London Mathematical Society, Volume 107, Issue 5 (2013), Pages 1004–1052

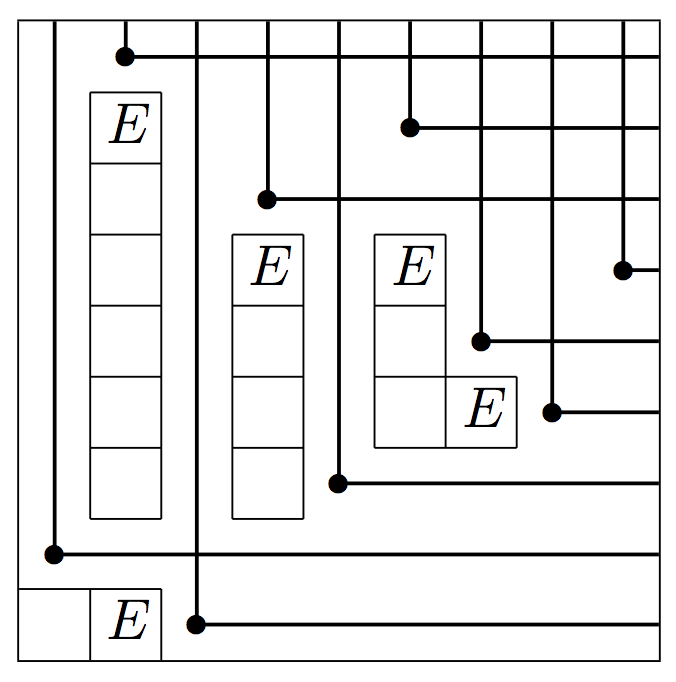  We characterize by pattern avoidance the Schubert varieties for GL_n which are local complete intersections (lci). For those Schubert varieties which are local complete intersections, we give an explicit minimal set of equations cutting out their neighborhoods at the identity. Although the statement of our characterization only requires ordinary pattern avoidance, showing that the Schubert varieties not satisfying our conditions are not lci appears to require working with more general notions of pattern avoidance. The Schubert varieties defined by inclusions, originally introduced by Gasharov and Reiner, turn out to be an important subclass, and we further develop some of their combinatorics. Applications include formulas for Kostant polynomials and presentations of cohomology rings for lci Schubert varieties.

• Refined inversion statistics on permutations

  Electronic Journal of Combinatorics, Volume 19 (2012)

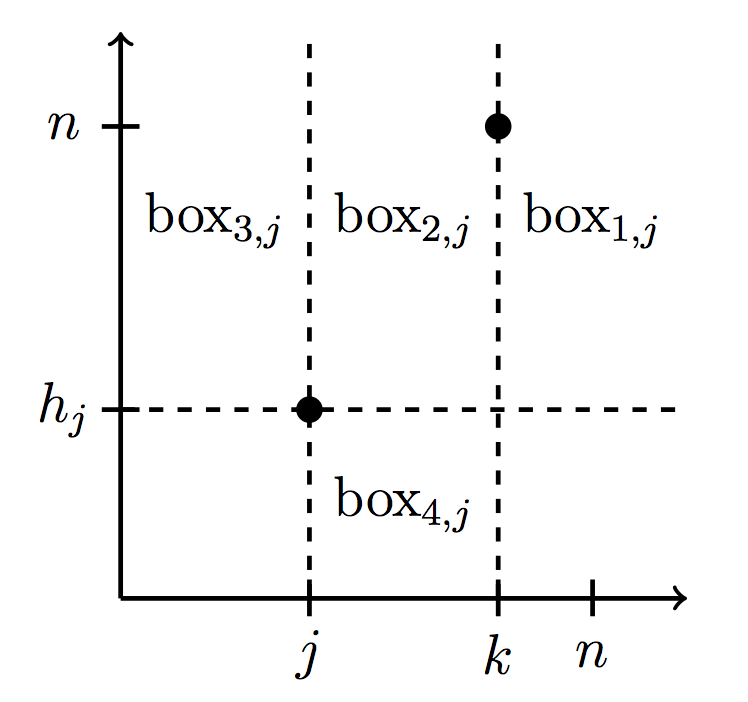  We introduce and study new refinements of inversion statistics for permutations, such as k-step inversions, (the number of inversions with fixed position differences) and non-inversion sums (the sum of the differences of positions of the non-inversions of a permutation). We also provide a distribution function for non-inversion sums, a distribution function for k-step inversions that relates to the Eulerian polynomials, and special cases of distribution functions for other statistics we introduce, such as (\leq k)-step inversions and (k_1,k_2)-step inversions (that fix the value separation as well as the position). We connect our refinements to other work, such as inversion tops that are 0 modulo a fixed integer d, left boundary sums of paths, and marked meshed patterns. Finally, we use non-inversion sums to show that for every number n>34, there is a permutation such that the dot product of that permutation and the identity permutation (of the same length) is n.

• Describing West-3-stack-sortable permutations with permutation patterns

  Séminaire Lotharingien de Combinatoire, Volume 67 (2012), Article B67d

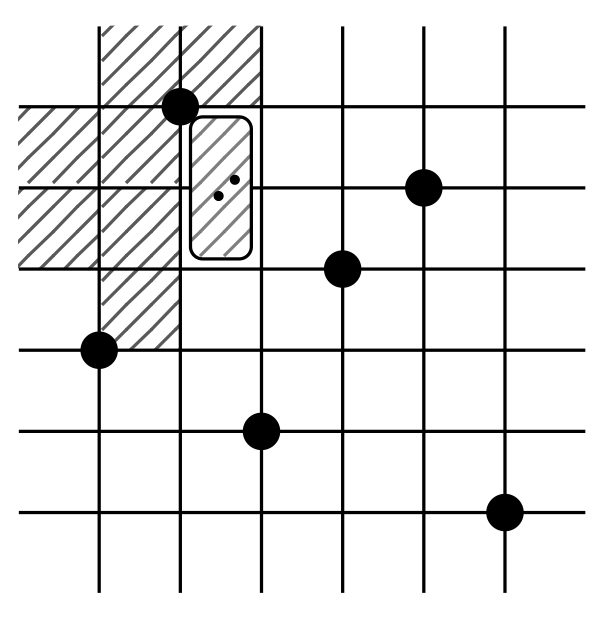  We describe a new method for finding patterns in permutations that produce a given pattern after the permutation has been passed once through a stack. We use this method to describe West-3-stack-sortable permutations, that is, permutations that are sorted by three passes through a stack. We also show how the method can be applied to the bubble-sort operator. The method requires the use of mesh patterns, introduced by Branden and Claesson (2011), as well as a new type of generalized pattern we call a decorated pattern.

• Word-representability of line graphs

  Open Journal of Discrete Mathematics, Volume 1, Number 2 (2011)

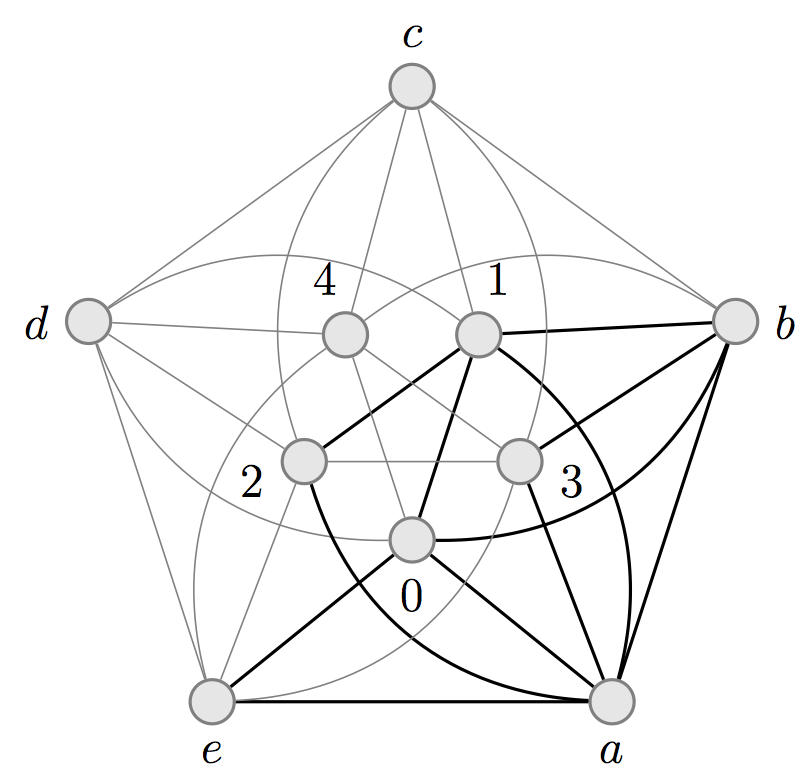  A graph G=(V,E) is representable if there exists a word W over the alphabet V such that letters x and y alternate in W if and only if (x,y) is in E for each x not equal to y. The motivation to study representable graphs came from algebra, but this subject is interesting from graph theoretical, computer science, and combinatorics on words points of view. In this paper, we prove that for n greater than 3, the line graph of an n-wheel is non-representable. This not only provides a new construction of non-representable graphs, but also answers an open question on representability of the line graph of the 5-wheel, the minimal non-representable graph. Moreover, we show that for n greater than 4, the line graph of the complete graph is also non-representable. We then use these facts to prove that given a graph G which is not a cycle, a path or a claw graph, the graph obtained by taking the line graph of G k-times is guaranteed to be non-representable for k greater than 3.

• A unification of permutation patterns related to Schubert varieties

  Pure Mathematics and Applications, Volume 22 (2011), Issue No. 2

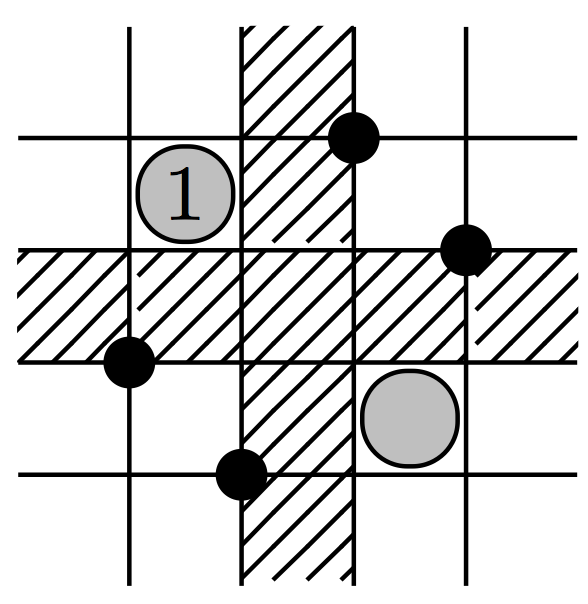  We obtain new connections between permutation patterns and singularities of Schubert varieties, by giving a new characterization of Gorenstein varieties in terms of so called bivincular patterns. These are generalizations of classical patterns where conditions are placed on the location of an occurrence in a permutation, as well as on the values in the occurrence. This clarifies what happens when the requirement of smoothness is weakened to factoriality and further to Gorensteinness, extending work of Bousquet-Melou and Butler (2007), and Woo and Yong (2006). We also show how mesh patterns, introduced by Branden and Claesson (2011), subsume many other types of patterns and define an extension of them called marked mesh patterns. We use these new patterns to further simplify the description of Gorenstein Schubert varieties and give a new description of Schubert varieties that are defined by inclusions, introduced by Gasharov and Reiner (2002). We also give a description of 123-hexagon avoiding permutations, introduced by Billey and Warrington (2001), Dumont permutations and cycles in terms of marked mesh patterns.