A unification of permutation patterns related to Schubert varieties
Pure Mathematics and Applications, Volume 22 (2011), Issue No. 2
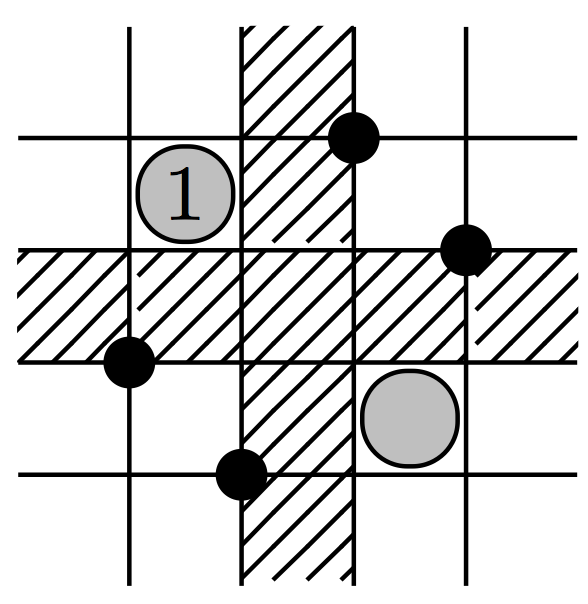We obtain new connections between permutation patterns and singularities of
Schubert varieties, by giving a new characterization of Gorenstein varieties in
terms of so called bivincular patterns. These are generalizations of classical
patterns where conditions are placed on the location of an occurrence in a
permutation, as well as on the values in the occurrence. This clarifies what
happens when the requirement of smoothness is weakened to factoriality and
further to Gorensteinness, extending work of Bousquet-Melou and Butler (2007),
and Woo and Yong (2006). We also show how mesh patterns, introduced by Branden
and Claesson (2011), subsume many other types of patterns and define an
extension of them called marked mesh patterns. We use these new patterns to
further simplify the description of Gorenstein Schubert varieties and give a
new description of Schubert varieties that are defined by inclusions,
introduced by Gasharov and Reiner (2002). We also give a description of
123-hexagon avoiding permutations, introduced by Billey and Warrington (2001),
Dumont permutations and cycles in terms of marked mesh patterns.