Enumeration of Permutation Classes and Weighted Labelled Independent Sets
Discrete Mathematics & Theoretical Computer Science, vol. 22 no. 2, Permutation Patterns 2019.
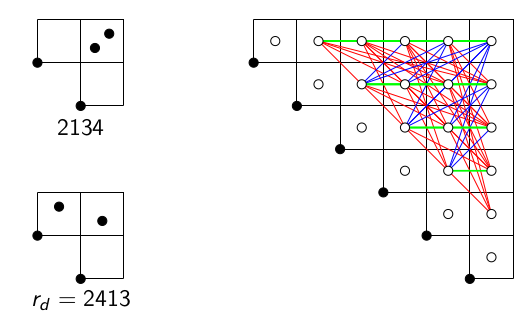 In this paper, we study the staircase encoding of permutations, which maps a
permutation to a staircase grid with cells filled with permutations. We consider
many cases, where restricted to a permutation class, the staircase encoding
becomes a bijection to its image. We describe the image of those restrictions
using independent sets of graphs weighted with permutations. We derive the
generating function for the independent sets and then for their weighted
counterparts. The bijections we establish provide the enumeration of permutation
classes. We use our results to uncover some unbalanced Wilf-equivalences of
permutation classes and outline how to do random sampling in the permutation
classes. In particular, we cover the classes Av(2314,3124) , Av(2413,3142),
Av(2413,3124), Av(2413,2134) and Av(2314,2143), as well as many subclasses.
In this paper, we study the staircase encoding of permutations, which maps a
permutation to a staircase grid with cells filled with permutations. We consider
many cases, where restricted to a permutation class, the staircase encoding
becomes a bijection to its image. We describe the image of those restrictions
using independent sets of graphs weighted with permutations. We derive the
generating function for the independent sets and then for their weighted
counterparts. The bijections we establish provide the enumeration of permutation
classes. We use our results to uncover some unbalanced Wilf-equivalences of
permutation classes and outline how to do random sampling in the permutation
classes. In particular, we cover the classes Av(2314,3124) , Av(2413,3142),
Av(2413,3124), Av(2413,2134) and Av(2314,2143), as well as many subclasses.
Download the paper
- Discrete Mathematics & Theoretical Computer Science, vol. 22 no. 2, Permutation Patterns 2019.
- arXiv