Turning cycle restrictions into mesh patterns via Foata's fundamental transformation
Submitted
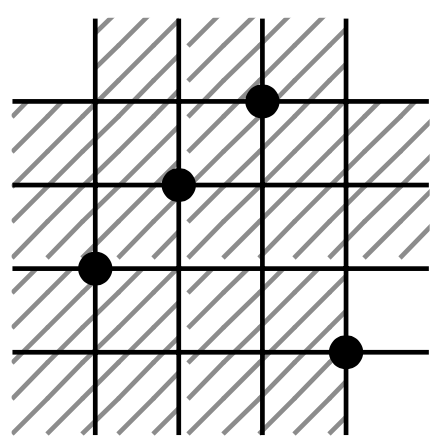An adjacent q-cycle is a natural generalization of an adjacent
transposition. We show that the number of adjacent q-cycles in a
permutation maps to the sum of occurrences of two mesh patterns under
Foata’s fundamental transformation. As a corollary we resolve
Conjecture 3.14 in the paper ‘‘From Hertzprung’s problem to
pattern-rewriting systems’’ by the first author.
This work was started at Schloss Dagstuhl (Leibniz-Zentrum fur Informatik), seminar 23121, and we thank the institute and the organizers for giving us the opportunity to participate.